Code
library(rstanarm)
library(bayesplot)
library(finalfit)
library(dplyr)
library(rms)
library(ggplot2)
library(gglm)
tryCatch(source('pander_registry.R'), error = function(e) invisible(e))Simple Linear Regression
Lecture 03
December 8, 2025
1 General Regression Setting
1.1 Two variable setting
Many statistical problems examine the association between two variables
Outcome variable (response variable,
dependent variable)Grouping variable (covariate, predictor variable,
independent variable)(While “dependent variable” and “independent variable” are commonly used, these imply that a modifiable independent variable is causing a dependent variable to change. We are fitting models focused on association, not causation.)
General goal is to compare distribution of the outcome variable across levels of the grouping variable
Groups are defined by the grouping variable
- Within each group, the grouping variable is constant
- Treatment and control groups
- Age: Continuous (days), broadly categorized (years), or wide categories (e.g. 0-18, 18-65, 65+)
In intro course, statistical analysis is characterized by two factors
Number of groups (samples)
If subjects in groups are independent
In the two variable setting, statistical analysis is more generally characterized by the grouping variable. If the grouping variable is
Constant: One sample problem
Binary: Two sample problem
Categorical: \(k\) sample problem (e.g. ANOVA)
Continuous: Infinite sample problem (analyzed with regression)
Regression thus extends the one- and two-sample problems up to infinite sample problems
Of course, in reality we never have infinite samples, but models that can handle this case are the ultimate generalization
Continuous predictors of interest
Continuous adjustment variables
Code
### Make a cholesterol and age dataframe. Set the random number seed so everything is reproducible
set.seed(19)
plotdata <- data.frame(age=c(63, 63, rep(65:80,15), rep(81:85,10), 86,86,86, 87,89, 90, 93, 95, 100),
chol=NA)
plotdata$chol <- 190 + .5*plotdata$age + rnorm(length(plotdata$age), 0, 15)
ggplot(plotdata, aes(x=age, y=chol)) + geom_point() + ylab("Cholesterol") + xlab("Age (years)") + theme_bw()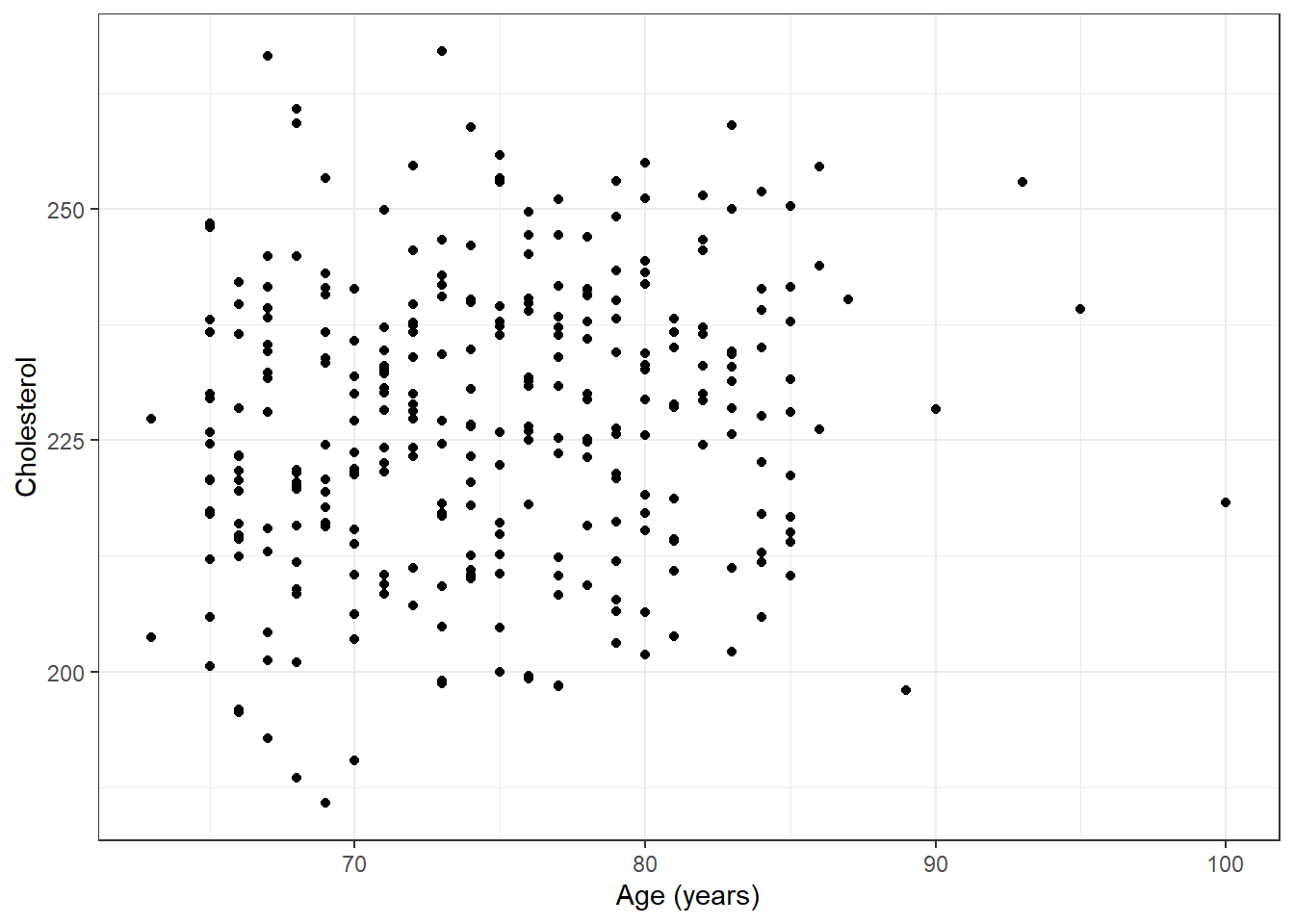
1.2 Regression versus two sample approaches
With a binary grouping variable, regression models reduce to the corresponding two variable methods
Linear regression with a binary predictor
- t-test, equal variance: Classic linear regression
- t-test, unequal variance: Linear regression with robust standard errors (approximately)
Logistic regression with a binary predictor
- (Pearson) Chi-squared test: Score test from logistic regression
Proportional odds regression with a binary predictor
- Wilcoxon Rank Sum Test
Cox (proportional hazards) regression with a binary predictor
- Log-rank test: Score test from Cox regression
1.3 Guiding principle
- Everything can be recast as a regression problem.
2 Motivating Problem: Cholesterol and Age
2.1 Definitions
Is there an association between cholesterol and age?
Scientific question: Does aging effect cholesterol?
Statistical question: Does the distribution of cholesterol differ across age groups?
Acknowledges variability in the response (cholesterol)
Acknowledges cause-effect relationship is uncertain
Association does not imply causation
- Any observed differences could be due to other factors. For example, the association could be with year of birth rather than age.
Continuous response variable: Cholesterol
Continuous grouping variable (predictor of interest): Age
- An infinite number of ages are possible
- We will not sample every possible age, and may round for simplicity
2.2 Simple Regression Model
Attempt to answer scientific question by assessing linear trends in average cholesterol
Estimate the best fitting line to average cholesterol within age groups
\[ E[\textrm{Chol} | \textrm{Age}] = \beta_0 + \beta_1 \times \textrm{Age} \]
The expected value of cholesterol given age is modeled using an intercept (\(\beta_0\)) and slope (\(\beta_1\))
An association exists if the slope is nonzero
A non-zero slope indicates that the average cholesterol will be different across different age groups
2.2.1 Descriptive plots of cholesterol and age
Code
ggplot(plotdata, aes(x=age, y=chol)) + geom_point() + ylab("Cholesterol") + xlab("Age (years)") + theme_bw() + geom_smooth()
Code
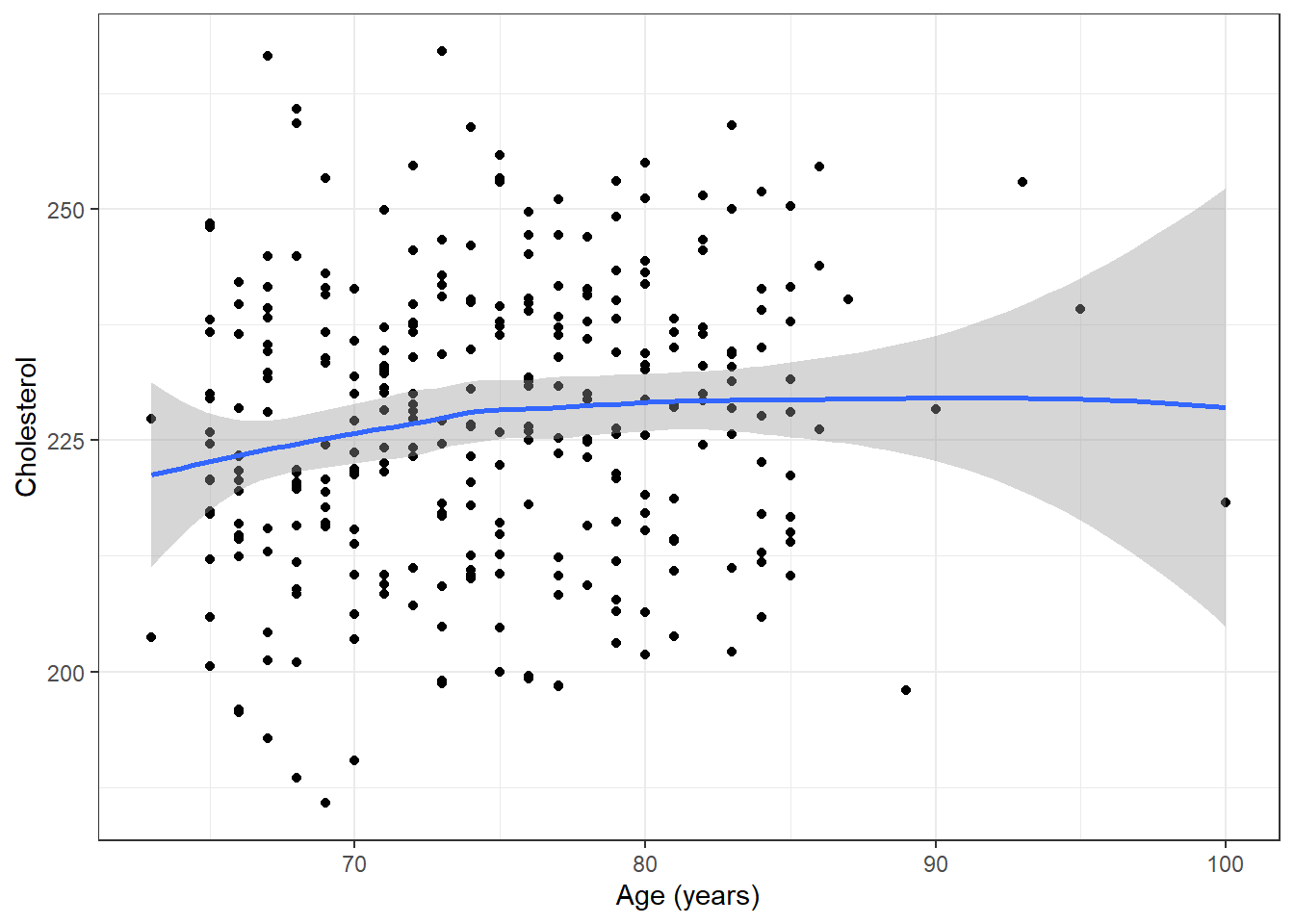
ggplot(plotdata, aes(x=age, y=chol)) + geom_point() + ylab("Cholesterol") + xlab("Age (years)") + theme_bw() + geom_smooth(method="lm")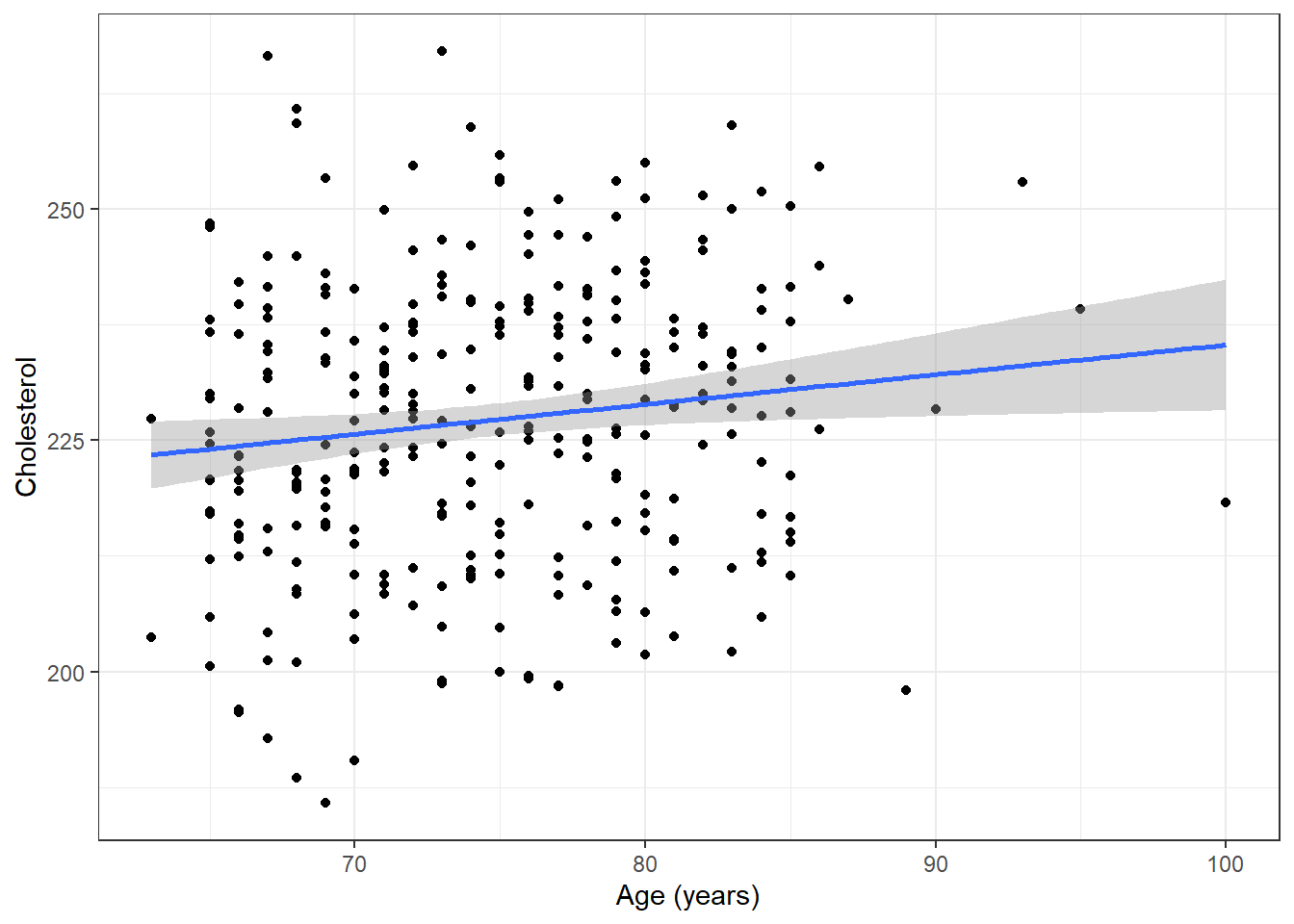
2.2.2 Simple linear regression model
The simple regression model produces an easy to remember (but approximate) rule of thumb.
“Normal cholesterol is 190 plus half your age”
\(E[\textrm{Chol} | \textrm{Age}] = 190 + 0.50 \times \textrm{Age}\)
Note that data were generated using this model. Estimates, below, will be different.
2.2.3 Frequentist Estimates and Interpretation
- Raw, unformatted estimates, model summary, and confidence intervals for age
Code
m.chol <- lm(chol ~ age, data=plotdata)
summary(m.chol)
Call:
lm(formula = chol ~ age, data = plotdata)
Residuals:
Min 1Q Median 3Q Max
-39.591 -10.524 -0.234 11.154 41.819
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 203.2259 10.3138 19.704 <2e-16 ***
age 0.3209 0.1375 2.333 0.0203 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 15.34 on 299 degrees of freedom
Multiple R-squared: 0.01788, Adjusted R-squared: 0.0146
F-statistic: 5.444 on 1 and 299 DF, p-value: 0.0203Code
confint.default(m.chol, "age") # Based on asymptotic Normality 2.5 % 97.5 %
age 0.051334 0.5904842\(E[\textrm{Chol} | \textrm{Age}] = 203.2 + 0.32 \times \textrm{Age}\)
- Using finalfit to create a nicer output table of the slope coefficient for age and confidence intervals
Code
explanatory = c("age")
dependent = 'chol'
label(plotdata$chol) <- "Cholesterol"
label(plotdata$age) <- "Age (years)"
finalfit(plotdata, dependent, explanatory) Dependent: Cholesterol unit value
Age (years) [63.0,100.0] Mean (sd) 227.2 (15.5)
Coefficient (univariable) Coefficient (multivariable)
0.32 (0.05 to 0.59, p=0.020) 0.32 (0.05 to 0.59, p=0.020)2.2.4 Bayesian Estimates and Interpretation
Bayesian approach to the linear model requires specifying
The model, e.g. a linear model with intercept and slope for age, Normally distributed errors and constant variance
Prior distributions on parameters
For the simple linear regression model, we have parameters \(\beta_0\), \(\beta_1\), and \(\sigma\).
For now, we will use default prior distributions that are are intended to be weakly informative in that they provide moderate regularization and help stabilize computation. See the STAN documentation for more details
Appropriate priors can be based on scientific considerations
Sensitivity analyses can evaluate the the robustness of finding to different prior assumptions
Output from Bayesian linear regression
Code
fit1 <- stan_glm(chol ~ age,
data=plotdata, family=gaussian(),
seed=1234,
refresh=0)
summary(fit1, digits=2, prob=c(.025, .5, .975))
Model Info:
function: stan_glm
family: gaussian [identity]
formula: chol ~ age
algorithm: sampling
sample: 4000 (posterior sample size)
priors: see help('prior_summary')
observations: 301
predictors: 2
Estimates:
mean sd 2.5% 50% 97.5%
(Intercept) 203.28 10.69 182.56 203.18 224.80
age 0.32 0.14 0.04 0.32 0.60
sigma 15.39 0.63 14.25 15.37 16.74
Fit Diagnostics:
mean sd 2.5% 50% 97.5%
mean_PPD 227.19 1.24 224.79 227.19 229.63
The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
MCMC diagnostics
mcse Rhat n_eff
(Intercept) 0.18 1.00 3721
age 0.00 1.00 3735
sigma 0.01 1.00 3469
mean_PPD 0.02 1.00 3911
log-posterior 0.03 1.00 1638
For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).- And a summary of the prior distributions used
Code
prior_summary(fit1, digits = 2)Priors for model 'fit1'
------
Intercept (after predictors centered)
Specified prior:
~ normal(location = 227, scale = 2.5)
Adjusted prior:
~ normal(location = 227, scale = 39)
Coefficients
Specified prior:
~ normal(location = 0, scale = 2.5)
Adjusted prior:
~ normal(location = 0, scale = 6)
Auxiliary (sigma)
Specified prior:
~ exponential(rate = 1)
Adjusted prior:
~ exponential(rate = 0.065)
------
See help('prior_summary.stanreg') for more detailsInterpretation
Slope for age is of primary scientific importance
A priori we assume that no association between age and cholesterol. Specifically, we assumed a Normal prior with location (mean) of 0 and scale (standard devation) of 6 for \(\beta_1\).
Conditional on the data, we estimate that for every 1 year increase in age, cholesterol increases by 0.32 mg/dl (95% credible interval 0.04 to 0.60).
2.2.5 Comparison of Frequentist and Bayesian interpretation of the slope
- Following was given by gpt-4.0 1
1 Query “Explain how a slope from simple linear regression is interpreted using language a college graduate could understand. Provide a Bayesian and Frequentist interpretation.” VUMC aiChat tool, GPT-4. Retrieved 12/28/2023.
In simple linear regression, the slope (often denoted as “b” or “beta”) is interpreted as the expected change in the dependent (or response) variable for a one-unit increase in the independent (or predictor) variable, assuming all other variables are held constant.
From a Frequentist perspective, the slope is considered a fixed but unknown value which is estimated from the sample data. If the slope is found to be 2, for instance, it would suggest that for every one-unit increase in our predictor variable, we expect, on average, a 2-unit increase in the response variable. This is based on the data at hand and is subject to sampling variability. Confidence intervals can be constructed around this estimate to provide a range of plausible values for this unknown fixed parameter. If a 95% confidence interval for the slope is (1.5, 2.5), it would suggest that we are 95% confident that the true slope falls within this range.
In contrast, a Bayesian approach treats the slope as a random variable. Rather than a single fixed value, the slope has a distribution of possible values. This distribution combines our prior beliefs about what the slope might be (prior distribution) and the observed data (likelihood). The resulting distribution (posterior distribution) reflects our updated belief about the slope after seeing the data. If the mean of the posterior distribution is 2, it suggests that, given the prior and the data, our best guess is that a one-unit increase in the predictor variable corresponds to a 2-unit increase in the response variable on average. A credible interval, say a 95% credible interval of (1.5, 2.5), suggests that there is a 95% probability that the true value of the slope falls within this range, given our prior and the observed data.
When to use Bayesian or frequentist approaches to estimation2
On many occasions, if one is careful in execution, both approaches to analysis will yield essentially equivalent inference
For small sample sizes, Bayesian approaches with carefully considered priors are often the only way to go because it is difficult to obtain well-calibrated frequentist intervals
For medium to large samples, unless there is strong prior information that one wants to incorporate, robust frequentist estimation using sandwich estimation is very appealing because its consistency is guaranteed under mild conditions
For highly complex models, a Bayesian approach is often the most convenient way to formulate the model, and computation under the Bayesian approach is the most straightforward
In summary, in many instances carefully considered Bayesian and frequentist approach will lead to similar scientific conclusions. My goal is describe the advantages and shortcoming of each approach, but a strong recommendation of one over the other is not given as there is often no reason for stating a preference.
2 Wakefield, Jon. Bayesian and Frequentist Regression Methods. Section 1.6, Executive Summary
2.3 Uses of Regression
Borrowing information
Use other groups to make estimates in groups with sparse data
Intuitively, 67 and 69 year olds would provide some relevant information about 68 year olds
Assuming a straight line relationship tells us about other, even more distant, individuals
If we do not want to assume a straight line, we may only want to borrow information from nearby groups
Locally weighted scatterplot smooth line (lowess) added to the previous figures
Splines discussed in future lectures
May not want to borrow too much information
Linear relationship is an assumption, with often low power to detect departures from linearity
Always avoid extrapolating beyond the range of the data (e.g. ages under 65 or over 100)
Defining “Contrasts”
Define a comparison across groups to use when answering scientific questions
If the straight line relationship holds, the slope is the difference in mean cholesterol levels between groups differing by 1 year in age
Do we want to assume that comparisons of 65 to 66 year old subjects are the same as comparisons of 95 to 96 year old subjects?
If a non-linear relationship, the slope is still the average difference in mean cholesterol levels between groups differing by 1 year in age
Slope is a (first order or linear) test for trend
2.4 Linear Regression Inference
Regression output provides
Estimates
Intercept: Estimated mean cholesterol when age is 0
Slope: Estimated average difference in average cholesterol for two groups differing by 1 year in age
Standard errors
Confidence intervals
P-values for testing
Intercept is zero (usually unimportant)
Slope is zero (test for linear trend in means)
(Frequentist) Interpretation
From linear regression analysis, we estimate that for each year difference in age, the difference in mean cholesterol is 0.32 mg/dL. A 95% confidence interval (CI) suggests that this observation is not unusual if the true difference in mean cholesterol per year difference in age were between 0.05 and 0.59 mg/dL. Because \(p = 0.02\), we reject the null hypothesis that there is no linear trend in the average cholesterol across age groups using a significance level, \(\alpha\), of \(0.05\).
3 Simple Linear Regression
3.1 Ingredients
Response
The distribution of this variable will be compared across groups
Linear regression models the mean of the response variable
Log transformation of the response corresponds to modeling the geometric mean
Notation: It is extremely common to use \(Y\) to denote the response variable when discussing general methods
Predictor
Group membership is measured by this variable
Notation
When not using mnemonics, will be referred to as the \(X\) variable in simple linear regression (linear regression with one predictor)
Later, when we discuss multiple regression, will refer to \(X_1, X_2, \ldots, X_p\) when there are up to \(p\) predictors
Regression Model
We typically consider a “linear predictor function” that is linear in the modeled predictors
Expected value (i.e. mean) of \(Y\) for a particular value of \(X\)
\(E[Y | X] = \beta_0 + \beta_1 \times X\)
In a deterministic world, a line is of the form \(y = mx + b\)
With no variation in the data, each value of \(y\) would like exactly on a straight line
Intercept \(b\) is values of \(y\) when \(x = 0\)
Slope \(m\) is the difference in \(y\) for a one unit difference in \(x\)
Statistics in not completely deterministic. The real world has variability
Response within groups is variable (people born on the same day will have different cholesterol levels!)
Randomness due to other variables impacting cholesterol
Inherent randomness
The regression line thus describes the central tendency of the data in a scatterplot of the response versus the predictor
Interpretation of regression parameters
Intercept \(\beta_0\): Mean \(Y\) for a group with \(X=0\)
Often \(\beta_0\) is not of scientific interest
May be out of the range of data, or even impossible to observe \(X=0\)
Slope \(\beta_1\): Difference in mean \(Y\) across groups differing in \(X\) by 1 unit
Usually measures association between \(Y\) and \(X\)
\(E[Y | X] = \beta_0 + \beta_1 \times X\)
Derivation of interpretation
Simple linear regression of response \(Y\) on predictor \(X\)
Mean of any arbitrary group can be derived from the equation \[ Y_i = \beta_0 + \beta_1 X_i \]
Interpretation determined by considering possible values of \(X\)
Model: \(E[Y_i | X_i] = \beta_0 + \beta_1 \times X_i\)
When \(X_i = 0\), \(E[Y_i | X_i = 0 ] = \beta_0\)
When \(X_i = x\), \(E[Y_i | X_i = x ] = \beta_0 + \beta_1 x\)
When \(X_i = x + 1\), \(E[Y_i | X_i = x + 1 ] = \beta_0 + \beta_1 x + \beta_1\)
We can use the above to get an equation for \(\beta_1\)
\[ E[Y_i | X_i = x + 1 ] - E[Y_i | X_i = x ] = \\ (\beta_0 + \beta_1 x + \beta_1) - (\beta_0 + \beta_1 x) \\ = \beta_1 \]
- Thus, \(\beta_1\) is the expected change in \(Y\) per one unit increase in \(x\)
3.2 Matrix Notation
Using scalars, the simple linear regression model can be written as
\(Y_i = \beta_0 + \beta_1 \times X_i + \epsilon_i\)
\(i = 1, \ldots, n\)
\(i\) indexes the independent sampling units (e.g. subjects)
\(n\) is the total number of independent sampling units
This formulauation drops the expected value notation, add in \(\epsilon_i\)
\(\epsilon_i\) are the “Residuals” or “Errors”
\(E[\epsilon_i] = 0\)
\(V[\epsilon_i] = \sigma^2\) (constant variance assumption)
- Matrix notation: \({\boldsymbol{Y}}= {\boldsymbol{X}}{\boldsymbol{\beta}}+ {\boldsymbol{\epsilon}}\)
\({\boldsymbol{Y}}= \left( \begin{array}{c} Y_1 \\ Y_2 \\ \vdots \\ Y_n \end{array} \right)_{n\times1}\) \({\boldsymbol{X}}= \left( \begin{array}{cc} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{array} \right)_{n\times2}\) \({\boldsymbol{\beta}}= \left( \begin{array}{c} \beta_0 \\ \beta_1 \\ \end{array} \right)_{2\times1}\) \({\boldsymbol{\epsilon}}= \left( \begin{array}{c} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{array} \right)_{n\times1}\)
\(E[{\boldsymbol{\epsilon}}] = {\boldsymbol{0}}\), where \({\boldsymbol{0}}= \left( \begin{array}{c} 0 \\ 0 \\ \vdots \\0 \end{array} \right)_{n\times1}\)
\(V[{\boldsymbol{\epsilon}}] = \sigma^2 {\boldsymbol{I}}\), where \({\boldsymbol{I}}= \left( \begin{array}{cccc} 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 \end{array} \right)_{n\times n}\)
\(E[{\boldsymbol{Y}}] = {\boldsymbol{X}}{\boldsymbol{\beta}}\)
I am using standard notation to indicate matrices/vectors and scalars
Boldface indicates a vector or matrix (\({\boldsymbol{Y}}\), \({\boldsymbol{X}}\), \({\boldsymbol{\beta}}\), \({\boldsymbol{\epsilon}}\), \({\boldsymbol{0}}\), \({\boldsymbol{I}}\))
Normal typeface indicates a scalar (\(Y_i\), \(x_i\), \(\beta_0\), \(\beta_1\), \(\epsilon_i\), \(0\), \(1\))
4 Example Analysis of BMI (Part 1)
Example analysis conducted in class involving BMI (response) with gender (predictor 1) and age (predictor 2)
This is “Lab 1” and will serve as an example of how future labs will proceed
5 Residuals
Often linear regression models are specified in terms of the response instead of the mean response
Include an error term in the model, \(\epsilon_i\)
Model \(Y_i = \beta_0 + \beta_1 X_i + \epsilon_i\)
The linear regression model is divided into two parts
The mean, or systematic, part (the “signal”)
The error, or random, part (the “noise”)
Residuals
\(\hat{\epsilon}_i = Y_i - \left(\hat{\beta_0} + \hat{\beta_1} X_i\right)\)
\(\hat{{\boldsymbol{\epsilon}}} = {\boldsymbol{Y}}- {\boldsymbol{X}}\hat{{\boldsymbol{\beta}}}\)
\(\hat{{\boldsymbol{\beta}}} = \left({\boldsymbol{X}}'{\boldsymbol{X}}\right)^{-1} \left({\boldsymbol{X}}'{\boldsymbol{Y}}\right)\)
The mean of the residuals is \(0\)
The standard deviation of the residuals is the “Root Mean Square Error”
In our example analysis of BMI and gender, the RMSE is exactly equal to the pooled estimate of the standard deviation from a two-sample, equal variance t-test
In our example analysis of BMI and age, the RMSE is the square root of the average variances across the age groups
In many textbooks, \(\epsilon_i \sim N(0, \sigma^2)\)
A common \(\sigma^2\) implies constant variance across all levels of the grouping variable, “homoscedasticity”
Normality of the residuals is a nice property, but it is not necessary (and rarely observed in practice)
We will discuss how lack of Normality and heteroscedasticity impact statistical inference
6 Assumptions and Inference with Linear Regression
6.1 The Big Three Assumptions
Most common uses of regression
Prediction: Estimating what a future value of \(Y\) will be based on observed \(X\)
Comparisons within groups: Describing the distribution of \(Y\) across levels of the grouping variable \(X\) by estimating the mean \(E[Y | X]\)
Comparisons across groups: Differences appear across groups if the regression parameter slope estimate \(\beta_1\) is non-zero
Valid statistical inference (CIs, p-values) about associations requires three general assumptions
Assumption 1: Approximately Normal distributions for the parameter estimates
Normal data or “large” N
It is often surprising how small “large” can be
Definition of large depends on the error distribution and relative sample sizes within each group
With exactly Normally distributed errors, only need one observation (or two to estimate a slope)
With very heavy tails, “large” can be very large
See Lumley, et al., Ann Rev Pub Hlth, 2002
Assumption 2: Independence of observations
Classic regression: Independence of all observation (now)
Robust standard errors: Correlated observations within identified clusters (later)
Assumption 3: Assumption about the variance of observations within groups
Classic regression: Homoscedasticity (equal variance across groups)
Robust standard errors: Allows for unequal variance across groups
6.2 Additional Assumptions for Additional Inference
Note that some textbooks will claim there are more than three assumptions. In truth, additional assumptions are not needed to make the aforementioned statistical inference about associations. However …
Valid statistical inference (CIs, p-values) about mean responses in specific groups requires a further assumption
Assumption 4: Adequacy of the linear model
If we are trying to borrow information about the mean from neighboring groups, and we are assuming a straight line relationship, the straight line needs to be true
No longer saying there is just a linear trend in the means, but now need to believe that all the means lie on a straight line
Note that we can model transformations of the measured predictor
For inference about individual observations (prediction intervals, P-values) in specific groups requires another assumption
Assumption 5: Assumptions about the distribution of the errors within each group (a very strong assumption)
Classically: Errors have the same Normal distribution within each grouping variable
Robust standard error will not help
Prediction intervals assume a common error distribution across groups (homoscedasticity)
Possible extension: Errors have the same distribution, but not necessarily Normal (rarely implemented in frequentist software)
Bootstrapping
Bayesian analysis
Other flexible approaches
6.2.1 Scenario 1: All model assumptions hold
Code
set.seed(1234)
n <- 200
regassumptions <- data.frame(x=seq(from=0, to=100, length=n))
# Linear model correct, Normal errors
regassumptions$y1 <- 5 + 0.2*regassumptions$x + rnorm(n,0,5)
# Linear model correct, Skewed errors
regassumptions$y2 <- 5 + 0.2*regassumptions$x + rlnorm(n,0,1)
# Linear model correct, errors increasing with predictor (so increasing with Y too)
regassumptions$y3 <- 5 + 0.2*regassumptions$x + rnorm(n,0,1+regassumptions$x*.1)
# Linear model incorrect, Normal error
regassumptions$y4<- 5 + 0.2*regassumptions$x + 0.02*(regassumptions$x)^2 + rnorm(n,0,5)
ggplot(regassumptions, aes(x=x, y=y1)) + geom_point() + geom_smooth(method="lm")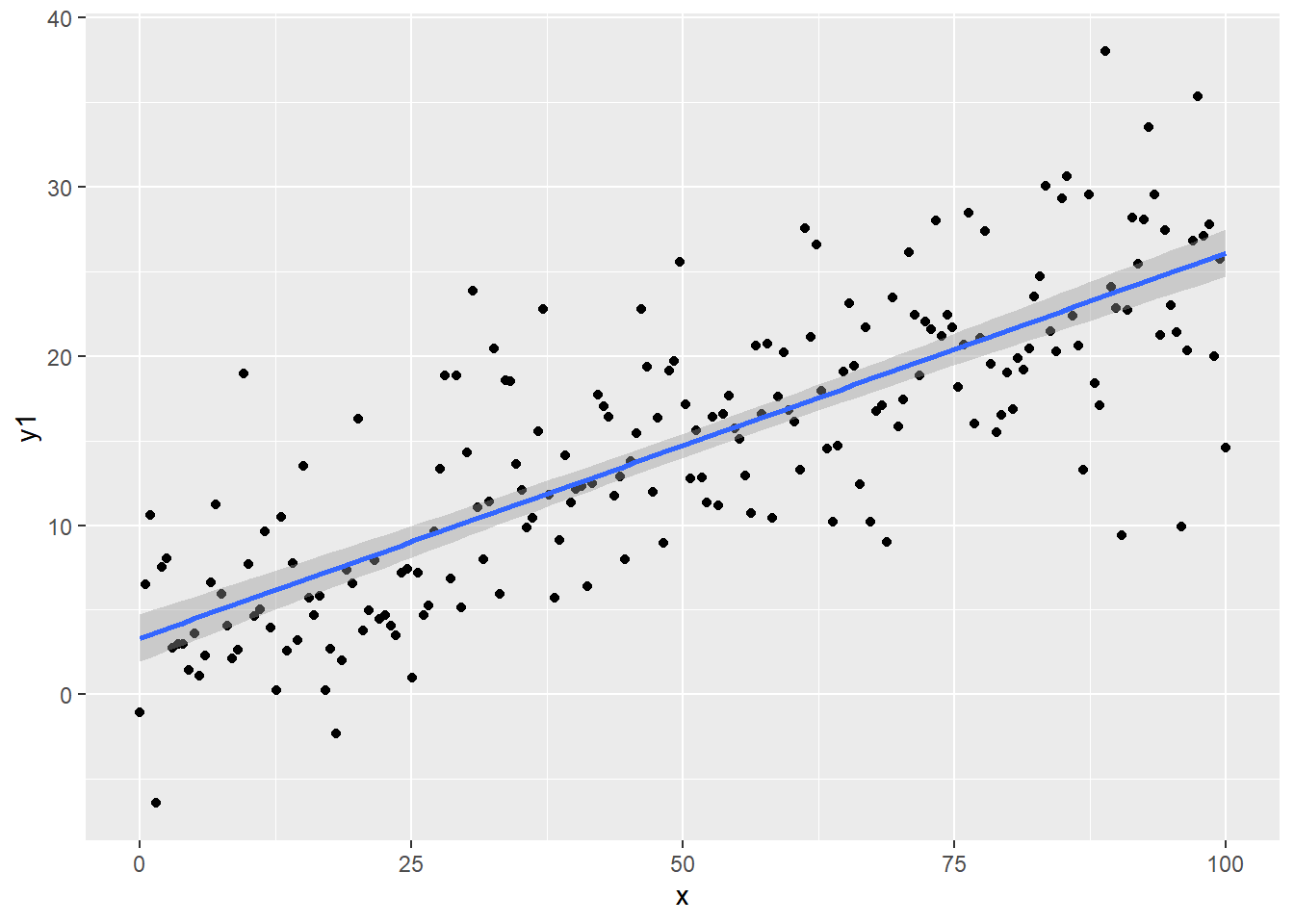
Code
model.y1 <- lm(y1 ~ x, data = regassumptions)
gglm(model.y1)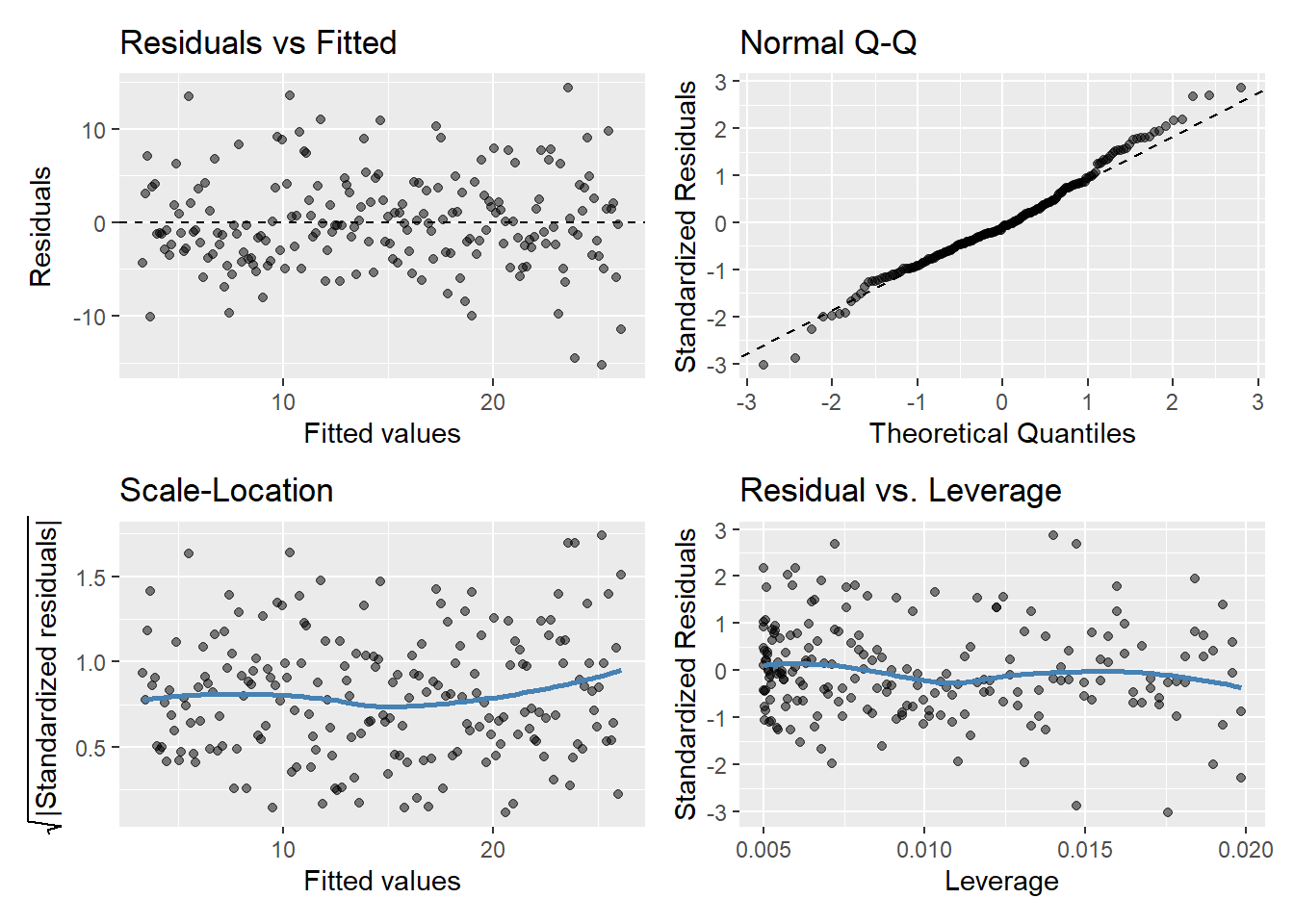
- Can estimate the mean of Y at a given value of X
- Can make inference about the association between X and Y (based on the slope)
- Can predict new values of Y given X
6.2.2 Scenario 2: Error distribution is not Normally distributed
Code
ggplot(regassumptions, aes(x=x, y=y2)) + geom_point() + geom_smooth(method="lm")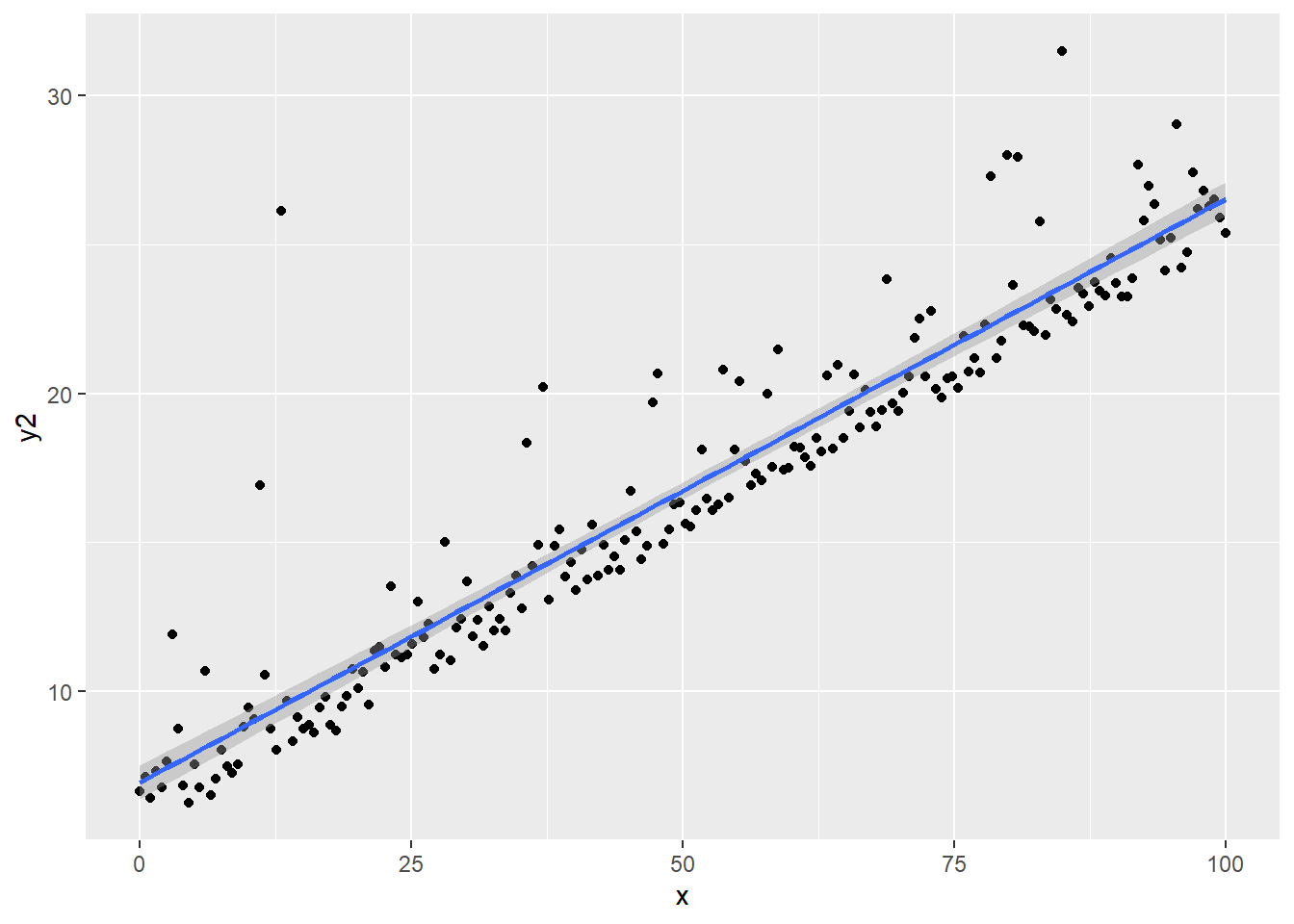
Code
model.y2 <- lm(y2 ~ x, data = regassumptions)
gglm(model.y2)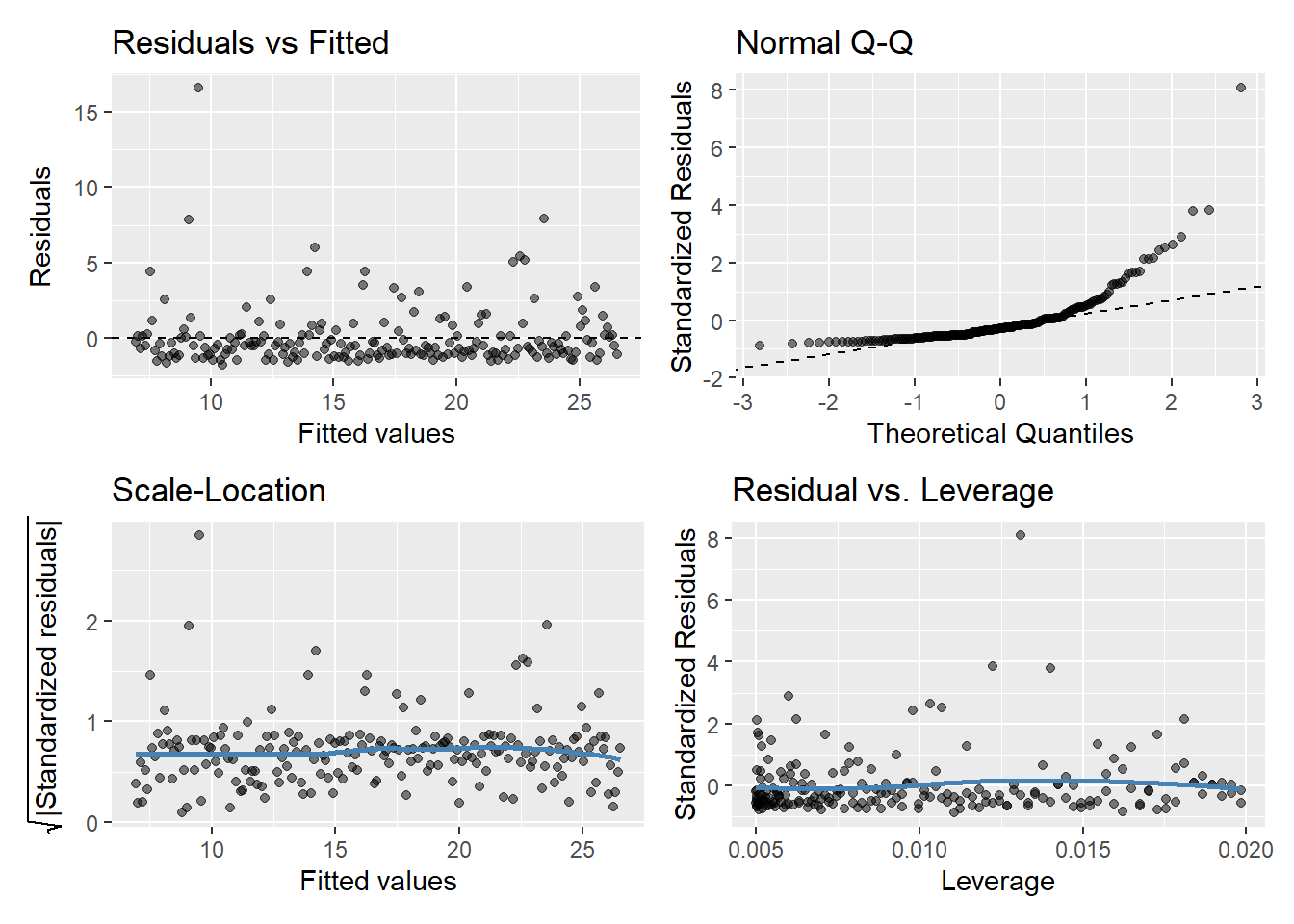
- If the sample size is large enough, we can estimate the mean of Y at a given value of X (Central Limit Theorem)
- If we use “robust” standard errors, we can make inference about the association between X and Y (based on the slope)
- Robust standard error relax the assumption of homoskedasticity/common variance
- We cannot predict new values of Y given X. This requires the correct error distribution.
6.2.3 Scenario 3: Variance increasing with predictor and expected value of Y (heteroskedasticity)
Code
ggplot(regassumptions, aes(x=x, y=y3)) + geom_point() + geom_smooth(method="lm")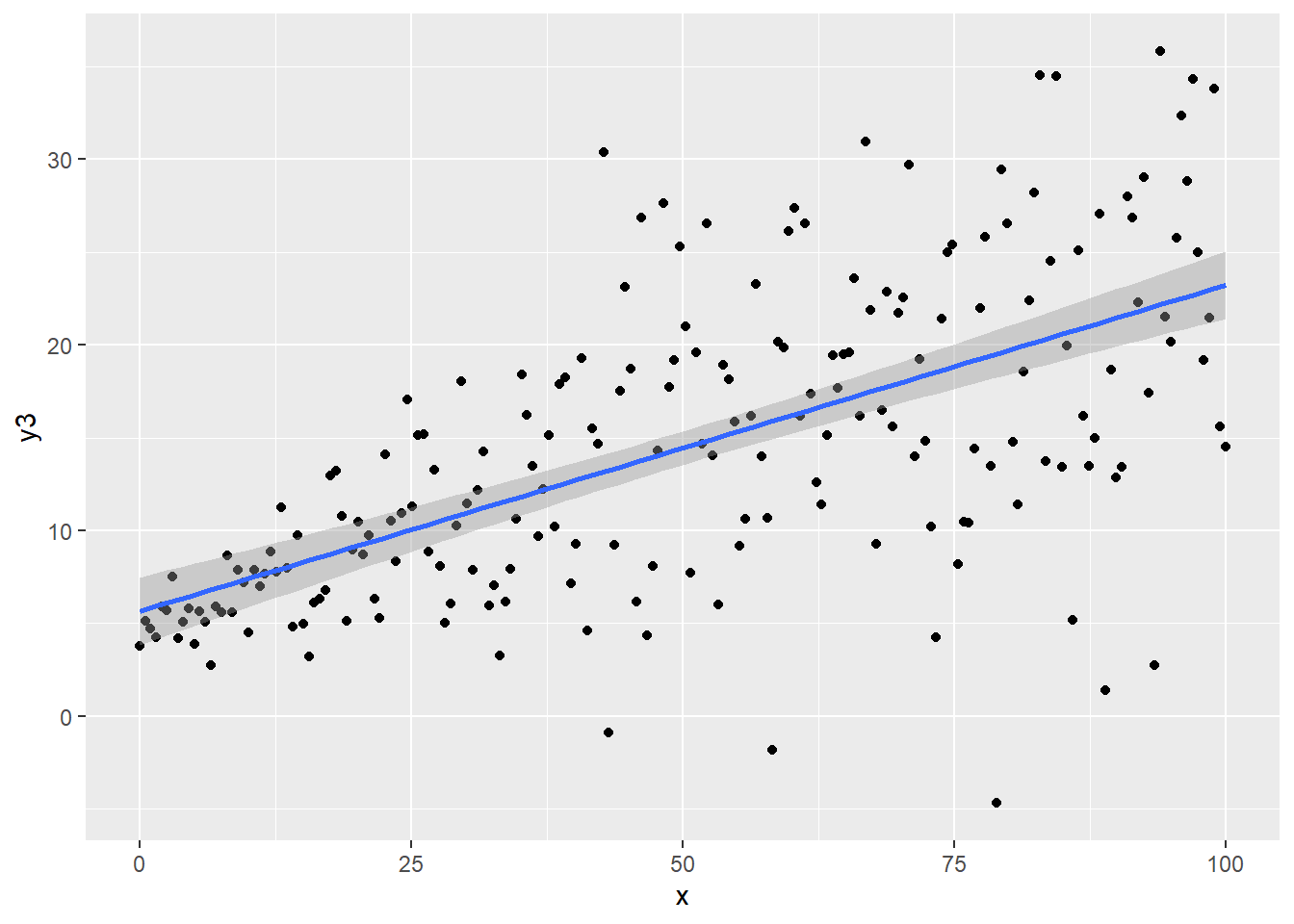
Code
model.y3 <- lm(y3 ~ x, data = regassumptions)
gglm(model.y3)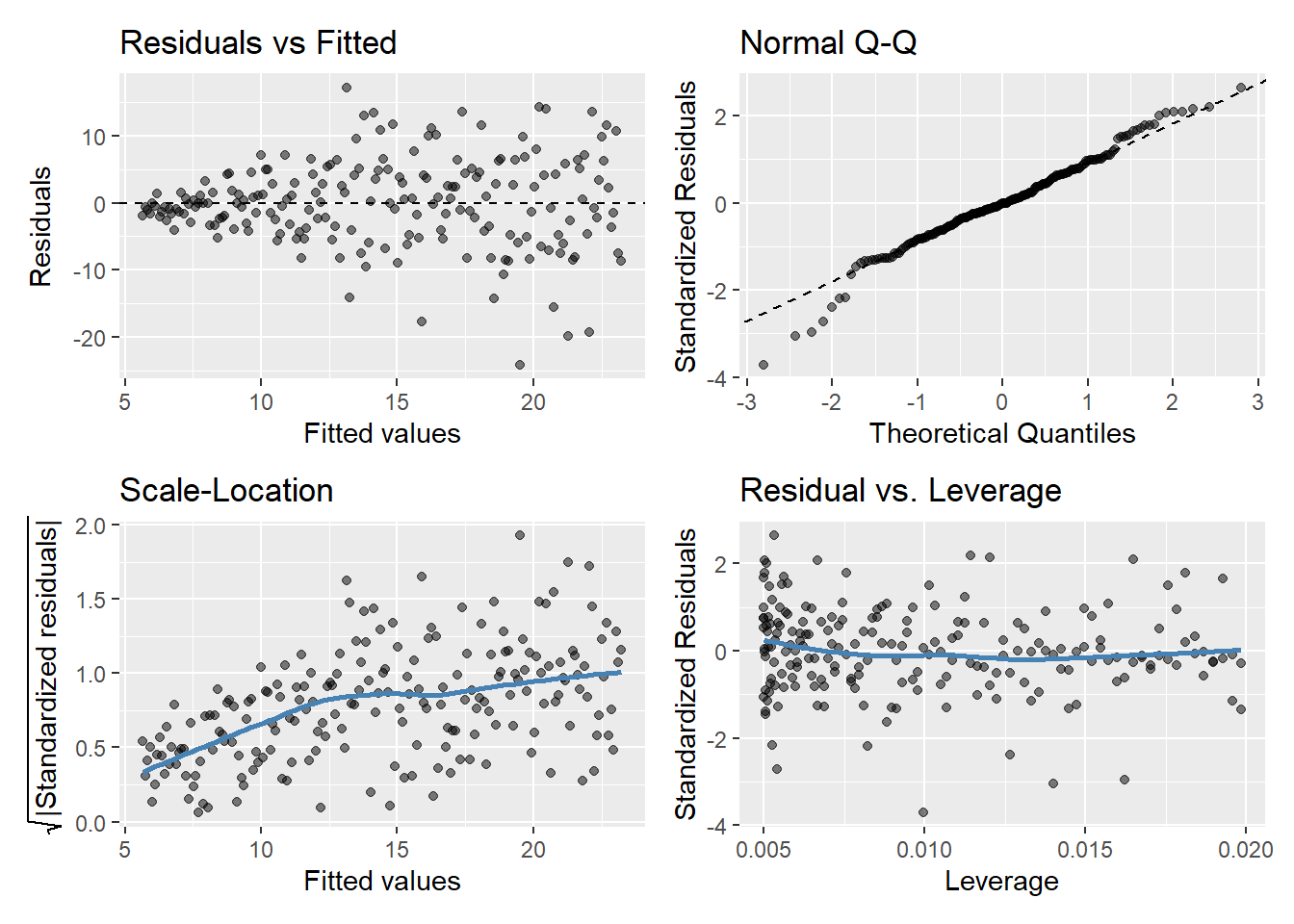
- If the sample size is large enough, we can estimate the mean of Y at a given value of X (Central Limit Theorem)
- If we use “robust” standard errors, we can make inference about the association between X and Y (based on the slope)
- Robust standard error relax the assumption of homoskedasticity/common variance
- We cannot predict new values of Y given X. This requires the correct error distribution (and mean model, but that is correct)
6.2.4 Scenario 4: Mean model incorrectly specified
Code
ggplot(regassumptions, aes(x=x, y=y4)) + geom_point() + geom_smooth(method="lm")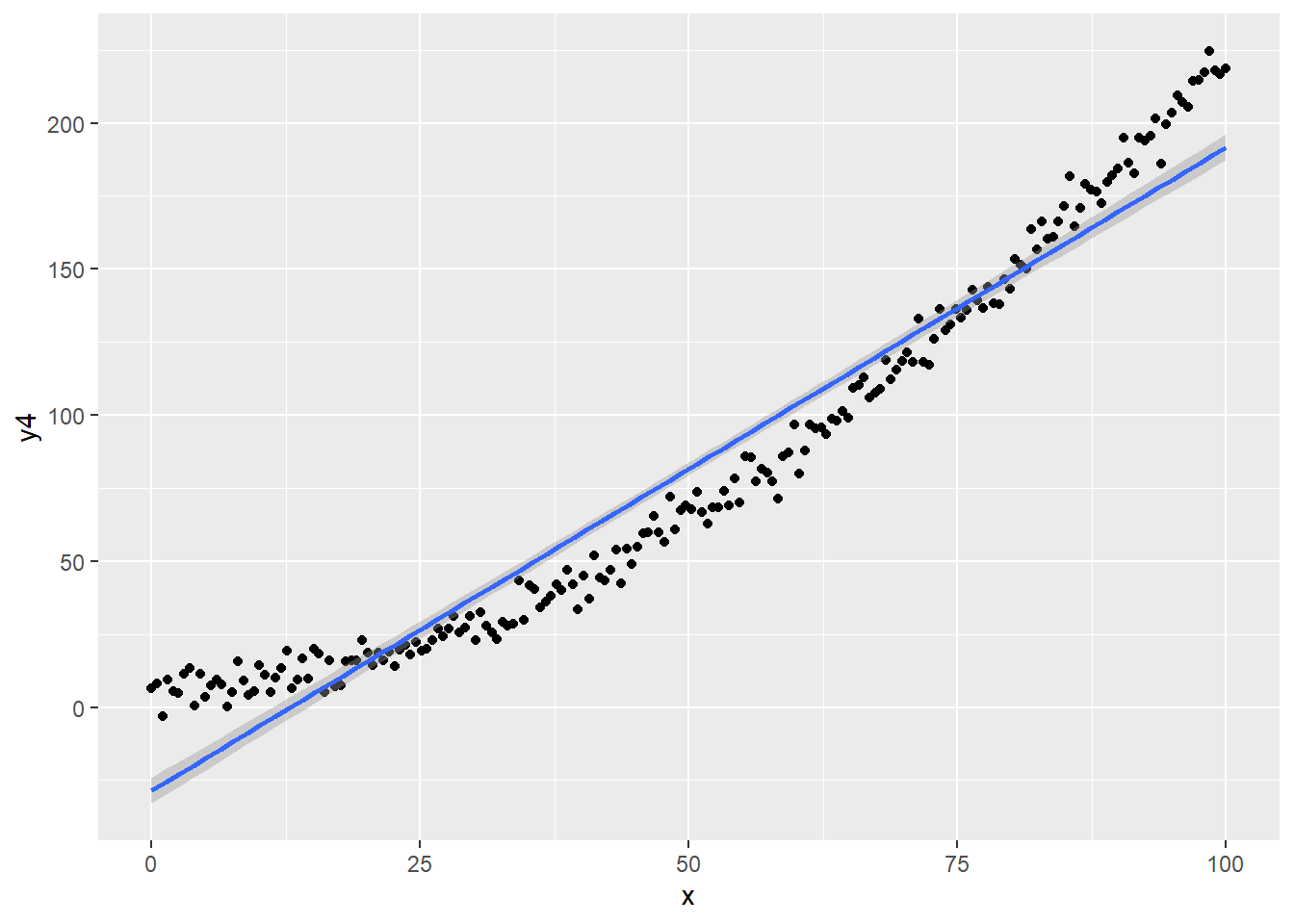
Code
model.y4 <- lm(y4 ~ x, data = regassumptions)
gglm(model.y4)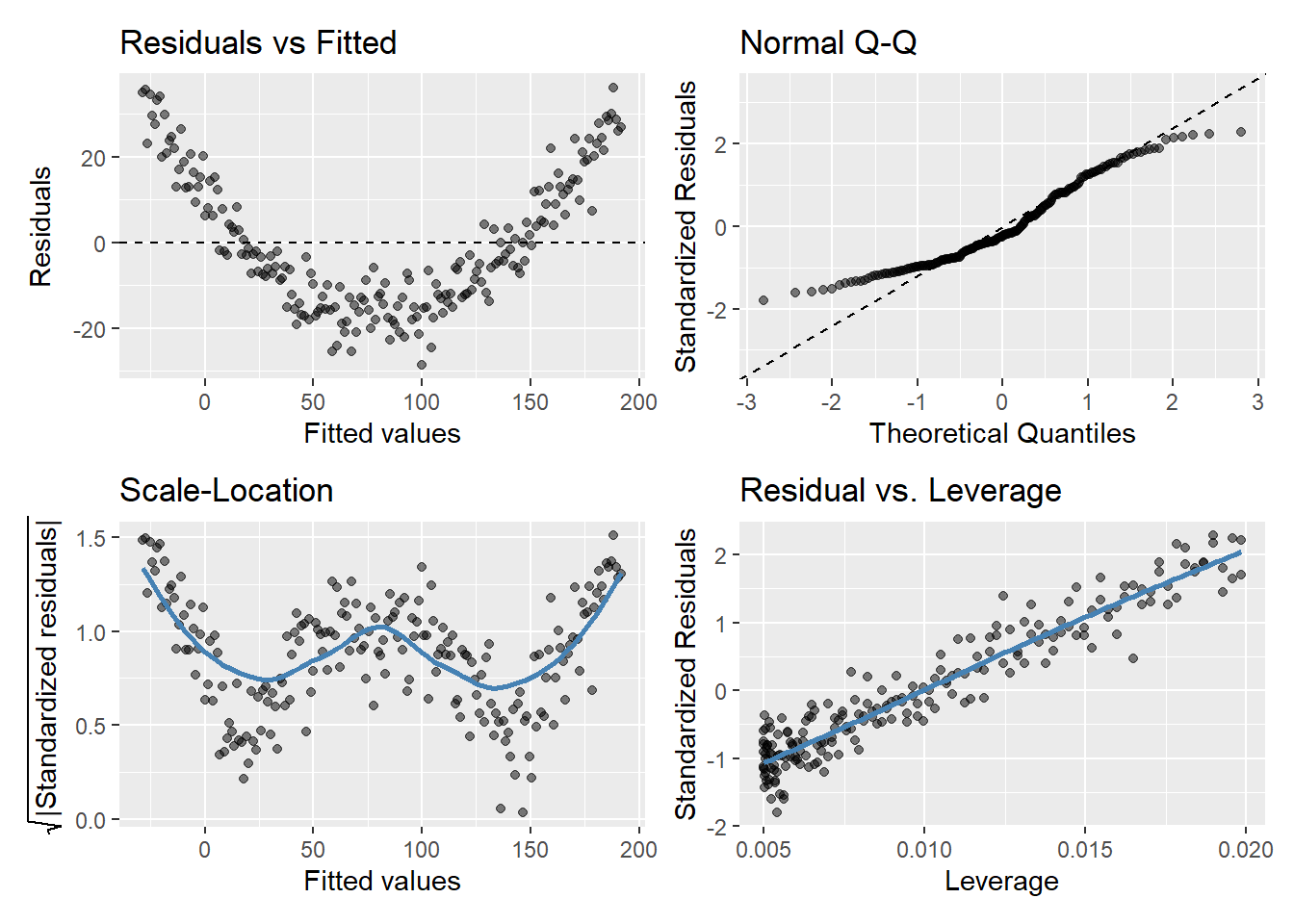
- Because our model is wrong, we cannot estimate the mean of Y at a given value of X. It will be biased, even if the sample size is large, the model will still be incorrect
- The good news is that we can fix our mean model to more flexibly model the association.
- Here, we have just included a single slope term to model the association with \(X\), \(E[Y|X] = \beta_0 + \beta_1*X\).
- The correct model in this simple example is \(E[Y|X] = \beta_0 + \beta_1*X + \beta_2*X^2\). Note that this model is still a “linear model”. A “linear model” is linear in the parameters (\(\beta_0\), \(\beta_1\), \(\beta_2\)). We can included the quadratic predictor \(X^2\) in the model and still have a model that is linear in the parameters.
- The good news is that we can fix our mean model to more flexibly model the association.
- If we use “robust” standard errors, we can make inference about the association between X and Y (based on the slope, \(\beta_1\))
- Robust standard error relax the assumption of homoskedasticity
- While the model is not a great fit, \(\beta_1\) may summarize a first-order trend
- We cannot predict new values of Y given X. This requires the correct mean model and error distribution.
6.2.5 Summary
Regression based inference about associations is far more trustworthy than estimation of group means or individual predictions.
There is much to be gained by using robust variance estimates
| Linearity | Homoskedasticity | Normality |
|---|---|---|
| Y | Y | Y |
| Y | Y | N |
| Y | N | Y |
| Y | N | N |
| N | Y | Y |
| N | Y | N |
| N | N | Y |
| N | N | N |
| \(\hat{\beta}\) | \(\hat{\textrm {Var}}_{NR}(\hat{\beta})\) | \(\hat{\textrm{ Var}}_R(\hat{\beta})\) |
|---|---|---|
| Y | Y | Y |
| Y | M2 | M2 |
| Y | N | Y |
| Y | N | M2 |
| M1 | N | M3 |
| M1 | N | M2,3 |
| M1 | N | M2 |
| M1 | N | M2,3 |
- 1 First-order trend, if appropriate
- 2 Approximately valid under large sample sizes
- 3 If \(X\) is random, but not if \(X\) is fixed
6.3 Interpreting “Positive” Results
Slope is statistically different from 0 using robust standard errors
Observed data is atypical of a setting with no linear trend in mean response across groups
Data suggests evidence of a trend toward larger (or smaller) means in groups having larger values of the predictor
(To the extent the data appears linear, estimates of the group means will be reliable)
6.4 Interpreting “Negative” Results
Many possible reasons why the slope is not statistically different from 0 using robust standard errors
There may be no association between the response and predictor
There may be an association, but not in the parameter considered (the mean response)
There may be an association in the parameter considered, but the best fitting line has zero slope
There may be a first order trend in the parameter considered, but we lacked the precision to be confident that it truly exists (a type II error)
7 Model Checking
Much statistical literature has been devoted to methods for checking the assumptions for regression models
My philosophy: Model checking is generally fraught with peril as it necessarily involves multiple comparisons
We cannot reliably use the sampled data to assess whether it accurately portrays the population
We are more worried about the data from the population that we might not have sampled
It is not so much the abnormal points that we see, but the ones that are hiding in the population that will make our model perform badly
But, do tend to worry more when we see a tendency to extreme outliers in the sample or clear departures from model assumptions
If we over-check our model and make adjustments to the model based on our observed data, we will inflate the type I error rate (i.e. will be more likely to claim statistical significance when it doesn’t really exist). We run the risk of creating a model that fits our data well but does not generalize.
Estimates are biased away from the null
Reported standard errors are too small
If we fish through the data, we will always find significant results
In clinical trials, often Phase II results are not able to be replicated in Phase III trials
Instead of extensive model checking, go back to our choices of inference when planning our analysis
Best to plan for unusual data
There is often little to be lost and much to be gained by using the robust standard error estimates
By using robust errors, avoids much of the need for model checking
Model checking is almost entirely data driven
Robust standard errors is a more logical scientific approach
Minimize the need to presume more knowledge than the question we are trying to answer
E.g., if we don’t know how the means might differ, why should we presume to know how the variances or the shape of the distribution might behave?
7.1 Residuals versus fitted values
Plot of \(\hat{\epsilon_i}\) versus \(\hat{y_i}\)
If assumptions hold, should be a random pattern about zero. See Figure 5 for example.
If you have a priori concerns about non-constant variance, this is one potential check
- E.g., it is fairly common for uncertainty to increase with outcome. See Figure 9 for the resulting “fan” pattern that would appear
7.2 Scale-location plot
The scale-location plot is very similar to residuals vs fitted values, and is used to evaluate the homoskedasticity assumption
It uses the square root of the absolute value of standardized residuals instead of plotting the residuals themselves
We want to check two things
That the best fit line is approximately horizontal. If it is, then the average magnitude of the standardized residuals isn’t changing much as a function of the fitted values.
That the spread around the fit line doesn’t vary with the fitted values. If so, then the variability of magnitudes doesn’t vary much as a function of the fitted values.
7.3 QQ plot
Used to evaluate Normality of the residuals
- If assumptions hold, points should lie on a 1:1 line
Plot of standardized residuals versus theoretical quantities from a N(0,1) distribution
If assumptions hold, the standardized residuals should be a random sample from a N(0,1) distribution
We can use quantiles of the Normal distribution to check how closely the observed matches the expected
- The 50th percentile of the residuals should be 0
- The 75th percentile of the residuals should be 0.67
- The 90th percentile of the residuals should be 1.28
- The 95th percentile of the residuals should be 1.64
- The 97.5th percentil of the residuals should be 1.96
Similar idea would be a histogram or density plot of the (standardized) residuals that could be visually evaluated for Normality
7.4 Residuals versus leverage
Used to check for outliers
Plot can help us to identify influential observations, if there are any
Influence differs from leverage. Not all outliers influence the regression coefficient estimates
8 Linear Regression with Robust Standard Error estimates
There are several libraries available in R for fitting models with robust error estimates
There are also several different flavors of robust estimators
For now, we are going to consider the default “Huber-White sandwich estimator”
In Stata, the Huber-White robust estimate of the standard error can be obtained using the ‘robust’ option
regress chol age, robust
In the following examples I provide estimates using classical linear regression and linear regression estimate using robust standard errors. For each of these example compare
Estimates of the intercept, \(\hat{\beta_0}\)
Estimates of the slope, \(\hat{\beta_1}\)
Estimates of the standard errors, \(\hat{\textrm{se}}(\hat{\beta_0})\) and \(\hat{\textrm{se}}(\hat{\beta_1})\)
8.1 Comparison when Normality, constant variance holds
8.1.1 Age and Cholesterol
Code
fit.ols <- ols(chol ~ age, data=plotdata, x=TRUE)
fit.olsLinear Regression Model
ols(formula = chol ~ age, data = plotdata, x = TRUE)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 301 LR chi2 5.43 R2 0.018
sigma15.3405 d.f. 1 R2 adj 0.015
d.f. 299 Pr(> chi2) 0.0198 g 2.344
Residuals
Min 1Q Median 3Q Max
-39.591 -10.524 -0.234 11.154 41.819
Coef S.E. t Pr(>|t|)
Intercept 203.2259 10.3138 19.70 <0.0001
age 0.3209 0.1375 2.33 0.0203 Code
robcov(fit.ols)Linear Regression Model
ols(formula = chol ~ age, data = plotdata, x = TRUE)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 301 LR chi2 5.43 R2 0.018
sigma15.3405 d.f. 1 R2 adj 0.015
d.f. 299 Pr(> chi2) 0.0198 g 2.344
Residuals
Min 1Q Median 3Q Max
-39.591 -10.524 -0.234 11.154 41.819
Coef S.E. t Pr(>|t|)
Intercept 203.2259 10.3790 19.58 <0.0001
age 0.3209 0.1378 2.33 0.0205 8.1.2 Scenario 1 dataset
Code
ols(y1 ~ x, data=regassumptions, x=TRUE)Linear Regression Model
ols(formula = y1 ~ x, data = regassumptions, x = TRUE)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 200 LR chi2 200.34 R2 0.633
sigma5.0531 d.f. 1 R2 adj 0.631
d.f. 198 Pr(> chi2) 0.0000 g 7.659
Residuals
Min 1Q Median 3Q Max
-15.2533 -3.2042 -0.4963 3.0693 14.4377
Coef S.E. t Pr(>|t|)
Intercept 3.3375 0.7119 4.69 <0.0001
x 0.2275 0.0123 18.47 <0.0001 Code
robcov(ols(y1 ~ x, data=regassumptions, x=TRUE))Linear Regression Model
ols(formula = y1 ~ x, data = regassumptions, x = TRUE)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 200 LR chi2 200.34 R2 0.633
sigma5.0531 d.f. 1 R2 adj 0.631
d.f. 198 Pr(> chi2) 0.0000 g 7.659
Residuals
Min 1Q Median 3Q Max
-15.2533 -3.2042 -0.4963 3.0693 14.4377
Coef S.E. t Pr(>|t|)
Intercept 3.3375 0.7002 4.77 <0.0001
x 0.2275 0.0132 17.20 <0.0001 8.2 Comparison when variance is increasing with predictor (Scenario 3)
Code
ols(y3 ~ x, data=regassumptions, x=TRUE)Linear Regression Model
ols(formula = y3 ~ x, data = regassumptions, x = TRUE)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 200 LR chi2 95.93 R2 0.381
sigma6.5232 d.f. 1 R2 adj 0.378
d.f. 198 Pr(> chi2) 0.0000 g 5.909
Residuals
Min 1Q Median 3Q Max
-24.1947 -3.7861 -0.1145 4.1816 17.2286
Coef S.E. t Pr(>|t|)
Intercept 5.6640 0.9191 6.16 <0.0001
x 0.1755 0.0159 11.04 <0.0001 Code
robcov(ols(y3 ~ x, data=regassumptions, x=TRUE))Linear Regression Model
ols(formula = y3 ~ x, data = regassumptions, x = TRUE)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 200 LR chi2 95.93 R2 0.381
sigma6.5232 d.f. 1 R2 adj 0.378
d.f. 198 Pr(> chi2) 0.0000 g 5.909
Residuals
Min 1Q Median 3Q Max
-24.1947 -3.7861 -0.1145 4.1816 17.2286
Coef S.E. t Pr(>|t|)
Intercept 5.6640 0.5955 9.51 <0.0001
x 0.1755 0.0153 11.49 <0.0001 8.3 Comparison when error variance is skewed to the right (Scenario 2)
Code
ols(y2 ~ x, data=regassumptions, x=TRUE)Linear Regression Model
ols(formula = y2 ~ x, data = regassumptions, x = TRUE)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 200 LR chi2 431.83 R2 0.885
sigma2.0635 d.f. 1 R2 adj 0.884
d.f. 198 Pr(> chi2) 0.0000 g 6.596
Residuals
Min 1Q Median 3Q Max
-1.8206 -1.1341 -0.6103 0.1731 16.6448
Coef S.E. t Pr(>|t|)
Intercept 6.9339 0.2907 23.85 <0.0001
x 0.1959 0.0050 38.95 <0.0001 Code
robcov(ols(y2 ~ x, data=regassumptions, x=TRUE))Linear Regression Model
ols(formula = y2 ~ x, data = regassumptions, x = TRUE)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 200 LR chi2 431.83 R2 0.885
sigma2.0635 d.f. 1 R2 adj 0.884
d.f. 198 Pr(> chi2) 0.0000 g 6.596
Residuals
Min 1Q Median 3Q Max
-1.8206 -1.1341 -0.6103 0.1731 16.6448
Coef S.E. t Pr(>|t|)
Intercept 6.9339 0.3526 19.67 <0.0001
x 0.1959 0.0056 35.18 <0.0001 9 Linear Regression and Correlation
9.1 Pearson’s Correlation
Notation
\(\rho\) signifies the population value
\(r\) (or \(\hat{\rho}\)) is the estimated correlation from data
Formula
\(r = \frac{\Sigma(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\Sigma(x_i - \bar{x})^2\Sigma(y_i - \bar{y})^2}}\)
Range: \(-1 \leq r \leq 1\)
Interpretation
Measures the linear relationship between \(X\) and \(Y\)
Correlation coefficient is a unitless index of strength of association between two variables (+ = positive association, - = negative, 0 = no association)
Can test for significant association by testing whether the population correlation is zero t = which is identical to the \(t\)-test used to test whether the population \(r\) is zero; \(\textrm{d.f.} = n-2\)
Use probability calculator for \(t\) distribution to get a 2-tailed \(P\)-value
Confidence intervals for population \(r\) calculated using Fisher’s \(Z\) transformation
\[Z = \frac{1}{2} \textrm{log}_\textrm{e} \left( \frac{1+r}{1-r} \right)\]
For large \(n\), \(Z\) follows a Normal distribution with standard error \(\frac{1}{\sqrt{n-3}}\)
To calculate a confidence interval for \(r\), first find the confidence interval for \(Z\) then transform back to the \(r\) scale
\[\begin{aligned} Z & = & \frac{1}{2} \textrm{log}_\textrm{e} \left( \frac{1+r}{1-r} \right) \\ 2*Z & = & \textrm{log}_\textrm{e} \left( \frac{1+r}{1-r} \right) \\ \textrm{exp}(2*Z) & = & \left( \frac{1+r}{1-r} \right) \\ \textrm{exp}(2*Z) * (1-r) & = & 1 + r \\ \textrm{exp}(2*Z) - r * \textrm{exp}(2*Z) & = & 1 + r \\ \textrm{exp}(2*Z) - 1 & = & r * \textrm{exp}(2*Z) + r \\ \textrm{exp}(2*Z) - 1 & = & r \left(\textrm{exp}(2*Z) + 1\right) \\ \frac{\textrm{exp}(2*Z) - 1}{\textrm{exp}(2*Z) + 1} & = & r \\ \end{aligned}\]
Example (Altman 89-90): Pearson’s \(r\) for a study investigating the association of basal metabolic rate with total energy expenditure was calculated to be \(0.7283\) in a study of \(13\) women. Derive a 95% confidence interval for \(r\)
\[Z = \frac{1}{2} \textrm{log}_\textrm{e} \left( \frac{1+r}{1-r} \right) = 0.9251\]
The lower limit of a 95% CI for \(Z\) is given by \(0.9251 + 1.96*\frac{1}{\sqrt{n-3}} = 0.3053\)
The upper limit is \(0.9251 + 1.96*\frac{1}{\sqrt{n-3}} = 1.545\)
A 95% CI for the population correlation coefficient is given by transforming these limits from the \(Z\) scale back to the \(r\) scale.
\[\frac{\textrm{exp}(2*0.3053) - 1}{\textrm{exp}(2*0.3053) + 1} \hspace{.5cm} \textrm{to} \hspace{.5cm} \frac{\textrm{exp}(2*1.545) - 1}{\textrm{exp}(2*1.545) + 1}\]
- Which gives a 95% CI from 0.30 to 0.91 for the population correlation
Code
fisher.z <- function(r) {.5 * log((1+r)/(1-r))}
fisher.z.inv <- function(z) {(exp(2*z)-1) / (exp(2*z)+1)}
fisher.z.se <- function(n) {1/sqrt(n-3)}
fisher.z.inv(fisher.z(0.7283)) #Should be original value[1] 0.7283Code
fisher.z(0.7283)[1] 0.9250975Code
fisher.z(0.7283)-1.96*fisher.z.se(13)[1] 0.3052911Code
fisher.z(0.7283)+1.96*fisher.z.se(13)[1] 1.544904Code
fisher.z.inv(fisher.z(0.7283)+c(-1.96, 1.96)*fisher.z.se(13))[1] 0.2961472 0.91294079.2 Relationship to regression
Pearson’s correlation (\(\rho\)) is directly related to linear regression
Correlation treats \(Y\) and \(X\) symmetrically, but we can relate
\(E[Y | X]\) as a function of \(X\)
\(E[Y | X] = \beta_0 + \beta_1 X\)
\(\beta_1 = \rho \frac{\sigma_Y}{\sigma_X}\)
\(E[Y | X]\): mean \(Y\) withing groups having equal \(X\)
\(\beta_1\): difference in mean \(Y\) per 1 unit difference in \(X\)
\(\rho\): true correlation between \(Y\) and \(X\)
\(\sigma_Y\): standard deviation of \(Y\)
\(\sigma_X\): standard deviation of \(X\)
More interpretable formulation of \(\rho\)
\(\rho \approx \beta \sqrt{\frac{\textrm{Var}(X)}{\beta^2\textrm{Var}(X) + \textrm{Var}(Y | X = x)}}\)
\(\beta\): slope between \(Y\) and \(X\)
\(\textrm{Var}(X)\): variance of \(X\) in the sample
\(\textrm{Var}(Y | X = x)\): variance of \(Y\) in groups having the same value of \(X\) (the vertical spread of data)
Correlation tends to increase in absolute value as
The absolute value of the slope of the line increases
The variance of data decreases within groups that share a common value of \(X\)
The variance of \(X\) increases
Scientific uses of correlation
The slope between \(X\) and \(Y\) is of scientific interest
The variance of \(Y\) given \(X=x\) is partly of scientific interest, but can also be impacted by restricting sampling to certain values of another variable
The variance of height given age is less if sampling just males than if sampling both sexes
The variance of \(X\) is often set by study design (which is often not of scientific interest)
Hypothesis tests for a nonzero correlation are exactly the same as a test for a nonzero slope in classical linear regression
The statistical significance of a given value of \(\rho\) depends only on the sample size
Correlation is more of a statistical measure than a scientific measure
10 Regression on Geometric Means: Log transformations
Geometric means of distributions are typically analyzed by using linear regression on the log transformed outcome
Used for inference under the following circumstances
We are (scientifically) interested in multiplicative rather than additive models
We want to down-weight the impact of outliers
The standard deviation of the response in a groups is proportional to the mean
- “Error is \(\pm 10\%\)” instead of “Error is \(\pm 10\)”
10.1 Interpretation of Parameters
Linear regression on the log transformed \(Y\)
Note that in statistics \(\textrm{log}\) almost always refers the the natural log (\(\textrm{log}_e\))
Model: \(E[\textrm{log} Y_i | X_i] = \beta_0 + \beta_1 \times X_i\)
When \(X_i = 0\): \(E[\textrm{log} Y_i | X_i = 0] = \beta_0\)
When \(X_i = x\): \(E[\textrm{log} Y_i | X_i = x] = \beta_0 + \beta_1 \times x\)
When \(X_i = x+1\): \(E[\textrm{log} Y_i | X_i = x + 1] = \beta_0 + \beta_1 \times x + \beta_1\)
Restate the model as log link for geometric mean
Model: \(\textrm{log GM}[Y_i | X_i] = \beta_0 + \beta_1 \times X_i\)
When \(X_i = 0\): \(\textrm{log GM}[Y_i | X_i = 0] = \beta_0\)
When \(X_i = x\): \(\textrm{log GM}[Y_i | X_i = x] = \beta_0 + \beta_1 \times x\)
When \(X_i = x+1\): \(\textrm{log GM}[Y_i | X_i = x + 1] = \beta_0 + \beta_1 \times x + \beta_1\)
Interpretation of parameters by back-transforming model
Model: \(\textrm{GM}[Y_i | X_i] = e^{\beta_0} \times e^{\beta_1 \times X_i}\)
When \(X_i = 0\): \(\textrm{GM}[Y_i | X_i = 0] = e^{\beta_0}\)
When \(X_i = x\): \(\textrm{GM}[Y_i | X_i = x] = e^{\beta_0} \times e^{\beta_1 \times x}\)
When \(X_i = x+1\): \(\textrm{GM}[Y_i | X_i = x + 1] = e^{\beta_0} \times e^{\beta_1 \times x} \times e^{\beta_1}\)
10.2 Example: FEV with Height
Question: How does FEV differ across height groups?
Scientific justification for summarizing with geometric mean
FEV is a volume
Height is a linear dimension
Each dimension of lung size is proportional to height
Standard deviation is likely proportional to height
Science: \(FEV \propto Height^3\) or \(\sqrt[3]{FEV} \propto Height\)
Statistics: \(\textrm{log}(FEV) \propto 3 \textrm{ log}(Height)\)
- Science dictates model choice
Statistical preference for (any) transformations of response
May transform to equal variance across groups
Homoscedasticity allows for easier inference
Statistical preference for a log transformation
Easier interpretation: multiplicative model
Compare groups using ratios
10.3 Log Transformed Predictors
Interpretation of log predictor and log link for response
Log link used to model the geometric mean of \(Y\)
Exponentiated slope estimates ratio of geometric means across groups
Log transformation of predictor compares groups with a \(k\)-fold difference in there measured predictors
Estimated ratio of geometric means
- \(\exp (\textrm{log}(k) \times \beta_1) = k^{\beta_1}\)
Interpretation of model
- \(\textrm{log GM}[FEV_i | log (height_i)] = -11.9 + 3.12 \times log(height_i)\)
Estimate ratio of geometric mean FEV for two groups differing by \(10\%\) in height (a 1.1 fold difference in height)
To find: Exponentiate \(1.1\) to the slope: \(1.1^{3.12} = 1.35\)
- “Group that is 10% taller is estimated to have a geometric mean FEV that is 1.35 times higher (35% higher)”
Why transform the predictor?
Typically chosen according to whether the data are likely to follow a straight line relationship
Linearity necessary to predict the values of the parameter in individual groups
Linearity is not necessary to estimate existence of an association
Linearity is not necessary to estimate a first order trend in the parameter across groups having the sampled distribution of the predictor
(Inference about these two questions will tend to be conservative if linearity does not hold)
Rarely do we know which transformation of the predictor provides the best linear fit
As always, there is significant danger in using the data to estimate the best transformation to use
If there is no association of any kind between the response and the predictor, a linear fit (with a zero slope) is correct
Trying to detect a transformation is thus an informal test for an association (multiple testing, which inflates type I error rate)
It is best to choose transformations of the predictor on scientific grounds
In practice, it is often true that mean functions are well approximated by a straight line over a small range of the data
Example: In the FEV dataset, the logarithm of height is approximately linear over the range of heights sampled (look at the plot)
We can often choose untransformed predictors when science would suggest a non-linear association
Can have major advantages in interpreting the results of the analysis
In the FEV example, it is far more natural to compare heights by difference than by ratios
- We would rather characterize two children as differing by 4 inches in height rather than as the 44 inch child being 10% taller than the 40 inch child
10.4 Looking Ahead to Multivariable Models
The relative importance of having the “true” transformation for a predictor depends on the statistical role
Predictor of Interest
Effect Modifiers
Confounders
Precision variables
We treat these variables different when planning our analysis
Predictor of Interest (should be pre-specified)
In general, don’t worry about modeling the exact association until you have even established an association (binary search)
Need to have a prespecified model for the POI
Searching for the best fit can inflate the type I error
Make most accurate, precise inference about the presence of the association first
Exploratory models can suggest models for future analyses
Effect Modifiers (difficult to do right anyway)
Modeling of effect modifiers is invariably just a test for the existence of an interaction
We rarely have a lot of precision to answer questions in subgroups of the data
Patterns of interaction can be so complex that it is unlikely that we will really capture the interactions across all subgroups in a single model
Typically, we would restrict future studies to analyses treating subgroups separately
Confounders (matters the most)
It is important to have an appropriate model of the association between the confounder and the response
Failure to accurately model the confounder means that some residual confounding will exist
However, searching for the best model may inflate the type I error for inference about the predictor of interest by overstating the precision of the study
Luckily, we rarely care about inference for the confounder, so we are free to use inefficient means of adjustment (e.g. a stratified analysis)
Precision Variables
When modeling precision variables, it is rarely worth the effort to use the “best” transformation
We usually capture the largest part of the added precision using crude models
We generally do not care about estimating association between the response and the precision variable
- Most often, precision variables represent known effects on the response
8.4 Comments
{{()}}{()}
Point estimates \(\hat{\beta_0}\) and \(\hat{\beta_1}\) were the same for robust and classical standard error
Point estimates \(\hat{\textrm{se}}(\hat{\beta_0})\) and \(\hat{\textrm{se}}(\hat{\beta_1})\) were different for robust and classical standard error
In general, it is hard to predict the effect of using robust standard errors
These were just a a couple of examples and do not constitute a thorough examination of the impact of using robust standard errors
When the model assumptions hold, for these two scenarios, robust standard error estimates were larger than classical standard error estimates
While this is not unexpected, to formally evaluate the amount of increase would require a statistical simulation
Simulate many datasets where the Normality and constant variance assumption holds
For each dataset, estimate \(\hat{\textrm{se}}(\hat{\beta_0})\) and \(\hat{\textrm{se}}(\hat{\beta_1})\)
Summarize the results
Approach will be covered in a future lab